Optionen – Teil 4: Die Griechen

Im vierten Teil der Beitragsserie „Optionen verstehen“ geht es um die Griechen. In diesem Beitrag erfährst du was die Griechen sind und was sie mit dem Thema Optionen zutun haben.

Die Welt der Optionen ist für Beginner im ersten Moment oft nicht ganz so leicht zu verstehen. Deshalb solltest du zuerst die vorherigen Beiträge der Beitragsserie über Optionen gelesen haben. Hier lernst du das notwendige Basiswissen und tust dir dann im weiteren Verlauf wesentlich leichter, das Thema zu durchleuchten.

Beitragsserie	Thema
1	Die Grundlagen
2	Put-Optionen
3	Call-Optionen

Was sind die Griechen?

Als Griechen, oder auch „Greeks“ genannt, werden die einzelnen Einflussfaktoren, die sich auf den Optionspreis auswirken, bezeichnet. Die Namensgebung kommt daher, dass jedem Einflussfaktor ein Buchstaben aus dem griechischen Alphabet zugeordnet wird. Die Griechen sind somit also Kennzahlen, die den Optionspreis bilden bzw. beeinflussen. Bisher haben wir gelernt, dass der Optionspreis im Wesentlichen durch den Kurs des Basiswertes, den Strike, der Laufzeit (Zeitwert) und der Volatilität gebildet wird. Genau diese Einflussfaktoren werden wiederum durch die Griechen dargestellt. Weitere Einflussfaktoren sind die Marktzinsen und eventuelle Dividendenzahlungen, die sich aus dem Underlying ergeben.

Diese Einflussfaktoren wirken auf den Optionspreis:

1. Aktueller Kurs des Basiswertes
2. Volatilität des Basiswertes
3. Laufzeit
4. Marktzinsen
5. Eventuelle Dividendenzahlungen des Basiswertes

Welche Griechen gibt es?

Beim Optionshandel haben die griechischen Kennzahlen eine große Bedeutung, weshalb es wichtig ist sich mit ihnen zu befassen. Durch die Griechen wissen wir von vornherein wie sich der Optionspreis während der Laufzeit verändern wird, wenn sich die Rahmenbedingungen verändern. Steigt z.B. die Volatilität während der Laufzeit an, beeinflusst dies wiederum direkt den Optionspreis. Die folgenden Griechen sollten wir kennen:

1. Delta – Das Delta beschreibt den Zusammenhang zwischen der Veränderung des Aktienkurses und dem Optionswert.
2. Gamma – Das Gamma beschreibt die Veränderung des Delta, wenn sich der Kurs der Aktie (Basiswert) verändert.
3. Theta – Das Theta beschreibt die Veränderung des Optionswertes, wenn sich die Restlaufzeit ändert.
4. Vega – Das Vega beschreibt die Veränderung des Optionswertes, wenn sich die Volatilität verändert.
5. Rho – Das Rho beschreibt wie sich der Wert einer Option verändert, wenn sich der risikolose Zinssatz verändert (unter risikolosem Zinssatz versteht man die Zinsen, welche für als sehr sicher geltende Anlagen, wie beispielsweise amerikanische oder schweizer Staatsanleihen, gezahlt werden) .

Diese fünf Griechen sind maßgeblich für die Bildung des Optionspreises und damit für den Wert einer Option verantwortlich. Verändert sich auch nur eine dieser Variablen, verändert sich auch der Optionspreis entsprechend. Je nachdem ob wir als Verkäufer oder als Käufer einer Option auftreten, haben die Veränderungen einen positiven oder negativen Effekt für uns.

Im Folgenden gehen wir detailliert auf die einzelnen griechischen Kennzahlen ein.

Das Delta

Das Delta ist wohl die bekannteste und gleichzeitig wichtigste griechische Kennzahl im Optionshandel. Wer sich auch nur ein bisschen mit dem Thema Optionen beschäftigt hat, wird mit Sicherheit schonmal vom Delta gehört haben. Das Delta beschreibt wie stark sich der Optionspreis verändert, wenn sich der Kurs des Basiswertes verändert. Das Delta bezieht sich dabei immer auf die Veränderung des Basiswertes um eine Einheit (1€).

Beispiel: Angenommen unsere Option hat ein Delta von 0,4. Wenn sich jetzt der Kurs unseres Basiswertes um eine Einheit (1€) verändert, dann wird sich der Optionspreis um 0,4€ verändern.

Je nach Optionsart kann das Delta zwischen 0 und -1 (Put) und 0 und +1 (Call) liegen.

Liegt der Kurs des Basiswertes genau am Strike der Option, liegt unsere Option am Geld (ATM). Ist unsere Option am Geld, haben wir ein Delta von genau +/- 0,5. Je weiter wir mit unserem Strike aus dem Geld sind, desto niedriger wird das Delta sein. Andersrum gilt, je weiter wir im Geld sind (die Option hat einen inneren Wert), desto größer wird das Delta sein.

Das Delta bei einem Call

Bei einem Call liegt das Delta immer zwischen 0 und +1. Je höher das Delta, desto größer ist die Veränderung des Optionspreises bei einer Kursveränderung des Basiswertes. Bei einem Delta von 1 verändert sich auch der Optionswert um jeweils 1€ pro 1€ Kursveränderung. Das bedeutet die Option macht genau die gleiche Bewegung wie der Aktienkurs. Steigt der Kurs, so steigt auch der Wert der Option um das Delta. Fällt der Kurs, so fällt der Wert der Option. Bei einem Delta von 0 hätte der Kurs des Basiswertes keinerlei Auswirkung auf den Optionspreis – der Optionspreis würde sich also überhaupt nicht verändern auch wenn sich der Aktienkurs verändert.

Beispiel: Das Delta einer Call-Option liegt bei 0,3. Wenn der Kurs des Basiswerts (Aktienkurs) jetzt um 1€ steigt wird der Wert der Option um 0,3€ steigen. Wenn der Kurs um 1€ fällt, wird der Wert der Option um 0,3€ fallen.

Das bedeutet im Umkehrschluss, wenn wir einen Call besitzen, also der Käufer der Call-Option sind, sollten wir auf ein möglichst hohes Delta achten und wenn wir der Call-Verkäufer (Stillhalter) sind sollten wir auf ein möglichst niedriges Delta achten.

Das Delta bei einem Put

Bei einem Put liegt das Delta hingegen immer zwischen 0 und -1. Der Optionspreis eines Puts entwickelt sich immer entgegengesetzt zum Kurs des Basiswertes, deshalb liegt das Delta auch immer im Negativbereich. Wenn der Kurs steigt, fällt der Optionspreis und wenn der Kurs fällt, steigt der Optionspreis um die Höhe des Deltas. Auch hier gilt, je höher das Delta, desto größer ist die Veränderung des Optionspreises bei einer Kursveränderung im Basiswert.

Beispiel: Das Delta liegt bei -0,3. Wenn der Kurs des Basiswerts (Aktienkurs) jetzt um 1€ steigt wird der Wert der Option um 0,3€ fallen. Wenn der Kurs um 1€ fällt, wird der Wert der Option um 0,3€ steigen.

Als Optionskäufer sollten wir wie beim Call, als auch beim Put, auf ein möglichst hohes Delta achten. Wir profitieren dann stärker von Kursveränderungen im Basiswert. Als Optionsverkäufer hingegen sollten wir Ausschau nach einem möglichst kleinen Delta halten. Das liegt daran, dass unser Gewinn auf die Prämie begrenzt ist und wir nicht weiter von einer Kursveränderung im Basiswert profitieren. Unser Ziel als Optionsverkäufer ist, dass die Option wertlos verfällt.

Als Optionsverkäufer sollte unser Delta, wenn möglich, kleiner 0,2 und als Optionskäufer größer 0,7 sein.

	Optionskäufer	Optionsverkäufer
hohes Delta	hilft	schadet
niedriges Delta	schadet	hilft

Mit dem Delta abschätzen, ob eine Option am Verfallstag im Geld sein wird

Eine weitere Verwendung des Deltas ist die schnelle Abschätzung, ob eine Option am Verfallstag im Geld sein wird. Dazu solltest du das Delta einfach mit 100 multiplizieren und schon weißt du wie hoch die Wahrscheinlichkeit ist, dass die Option am Verfallstag ausgeübt wird.

Beispiel: Das Delta deiner Option liegt bei 0,3. Dies bedeutet, dass deine Option eine Wahrscheinlichkeit von 30% (0,3 x 100) hat, am Verfallstag im Geld zu sein und damit ausgeübt zu werden. Umgekehrt bedeutet es auch, dass die Option mit einer Wahrscheinlichkeit von 70% nicht im Geld sein wird und entsprechend wertlos verfällt.

Wichtig dabei ist zu verstehen, dass es sich hierbei lediglich um Wahrscheinlichkeiten handelt. Relevante Faktoren wie wichtige Unternehmensmeldungen, Chartanalyse oder Fundamentaldaten der Aktie werden hierbei nicht berücksichtigt.

Übrigens: das Delta bleibt nicht konstant. Wenn sich der Kurs des Basiswertes verändert, verändert sich auch das Delta in die entsprechende Richtung. Wie stark sich eine Veränderung im Kurs des Basiswertes auf das Delta auswirkt wird von der Kennzahl Gamma angegeben.

• Je höher das Delta, desto stärker macht die Option die Preisbewegungen des Basiswertes mit.
• Das Delta bleibt nicht konstant, sondern ändert sich, wenn sich der Kurs des Basiswertes verändert.
• Ein Call hat immer ein positives Delta, ein Put ein Negatives.
• Sind wir Optionskäufer, dann suchen wir Optionen mit einem möglichst hohen Delta.
• Sind wir Optionsverkäufer, dann suchen wir Optionen mit einem möglichst geringen Delta.
• Des Weiteren dient das Delta zur schnellen Einschätzung mit welcher Wahrscheinlichkeit eine Option am Verfallstag ausgeübt werden wird.

Das Gamma

Während das Delta mathematisch gesehen die erste Ableitung des Preises des Basiswertes ist, ist das Gamma die zweite Ableitung vom Preis des Basiswertes (Aktienkurs). Wir haben bereits gelernt, dass das Delta nicht konstant bleibt und sich verändert, wenn sich der Kurs des Basiswertes verändert. Das Gamma beschreibt genau diese Veränderung, nämlich wie stark sich das Delta verändert, wenn sich der Kurs des Basiswertes um eine Einheit (1€) verändert. Oder anders ausgedrückt: das Gamma zeigt uns wie empfindlich sich das Delta bei Kursänderungen verändert.

Beispiel: Wir haben eine Call Option mit einem Delta von 0,4 und ein Gamma von 0,05. Steigt jetzt der Preis des Basiswertes um 1€, wird zum einen der Optionspreis um 0,4€ (aktuelles Delta) steigen und auch das Delta selbst wird steigen, nämlich um die Höhe des Gammas, sprich um 0,05. Nach dem Kursanstieg liegt das neue Delta somit bei 0,4 + 0,05 = 0,45. Das bedeutet, wenn der Kurs erneut um 1€ steigt, verändert sich der Optionspreis jetzt nicht mehr um 0,4€, sondern um 0,45€.

Das Gamma ist am höchsten, wenn sich eine Option direkt am Geld (ATM) befindet, also wenn der Strike der Option gleich dem Aktienkurs ist. Je weiter eine Option im Geld (ITM) oder aus dem Geld (OTM) ist, desto geringer ist das Gamma.

Genau wie das Delta bleibt auch das Gamma niemals konstant, sondern verändert sich ebenfalls, wenn sich der Kurs des Basiswertes verändert. Wie sich das Gamma und schließlich auch das Delta durch Kursveränderungen im Basiswert verändert zeigt dir folgende Tabelle.

Veränderung Kurs des Basispreises (Aktienkurs)	Call	Put
Kurs steigt um 1€	das Delta und das Gamma steigt an	das Delta und das Gamma sinkt
Kurs fällt um 1€	das das Delta und das Gamma sinkt	das Delta und das Gamma steigt

Wie auch beim Delta sollten Optionsverkäufer auf ein möglichst hohes Gamma achten, um möglichst stark von Preisveränderungen im Basiswert zu profitieren. Bedenke allerdings auch, dass die starke Preisveränderung genauso stattfindet, wenn sich der Kurs in die nicht erwünschte Richtung entwickelt. Optionsverkäufer hingegen sollten nach einem möglichst kleinen Gamma Ausschau halten, damit sich der Optionspreis bei Kursveränderungen im Basiswert möglichst wenig verändert. Zur Erinnerung: als Optionsverkäufer (Stillhalter) ist unser Gewinn auf die Höhe der Prämie begrenzt. Somit profitieren wir auch nicht von starken Kursveränderungen. Bestenfalls bleibt der Kurs über die gesamte Laufzeit konstant und verändert sich kaum.

Das Vega – Einfluss der Volatilität

In den vorangegangenen Beiträgen zum Thema Optionen haben wir bereits gelernt, dass die Volatilität eine entscheidende Rolle bei der Optionspreisbildung einnimmt. Genauer gesagt die implizite Volatilität. Diese drückt die Erwartung der Marktakteure hinsichtlich der zukünftigen Volatilität (Schwankungsbreite) des Basiswertes aus. Die Volatilität ist also ein Indikator zur Bestimmung der Unsicherheit über die zukünftige Marktentwicklung. Eine hohe implizite Volatilität (IV) sagt aus, dass die Marktteilnehmer von starken Kursschwankungen ausgehen, während man bei einer niedrigen IV von geringeren Schwankungen ausgeht. Die implizite Volatilität wird durch die Kennzahl Vega wiedergegeben.

Das Vega gibt an, um wie viel sich der Optionspreis verändert, wenn sich die implizite Volatilität des Basiswertes um 1% verändert. Je höher die implizite Volatilität des Basiswertes, desto höher ist auch das Vega und entsprechend der Preis der Option.

Der Optionspreis ist bei Aktien mit hoher Volatilität höher, da die Marktteilnehmer bereit sind mehr Geld für Absicherungen (höhere Prämien) zu bezahlen. Als Stillhalter (Optionsverkäufer) profitieren wir entsprechend von einer sinkenden Volatilität. Wir sollten deshalb beim Verkaufen von Optionen auf ein möglichst hohes Vega bzw. eine hohe IV achten und profitieren dann, wenn diese während der Laufzeit unserer Option fällt, weil der Wert der Option dadurch sinkt.

Optionskäufer hingegen sollten auf ein niedriges Vega bzw. eine niedrige IV achten, da durch einen Anstieg der IV der Wert der Option steigt und dies einen Gewinn für den Optionskäufer darstellt.

Das Theta – Der Zeitwertverfall

Eine weitere Einflussgröße die sich direkt auf den Optionspreis auswirkt, ist die Restlaufzeit der Option. Wir haben bereits gelernt, dass sich der Wert einer Option aus dem inneren Wert und dem Zeitwert zusammensetzt. Der Zeitwert nimmt immer weiter ab, je näher der Verfallstag rückt. Das Theta gibt dabei an, um wie viel sich der Zeitwert der Option pro Tag verringert.

Merke: Das Theta gibt an, um wie viel sich der Preis der Option verändert, wenn sich die Laufzeit der Option um einen Tag verkürzt.

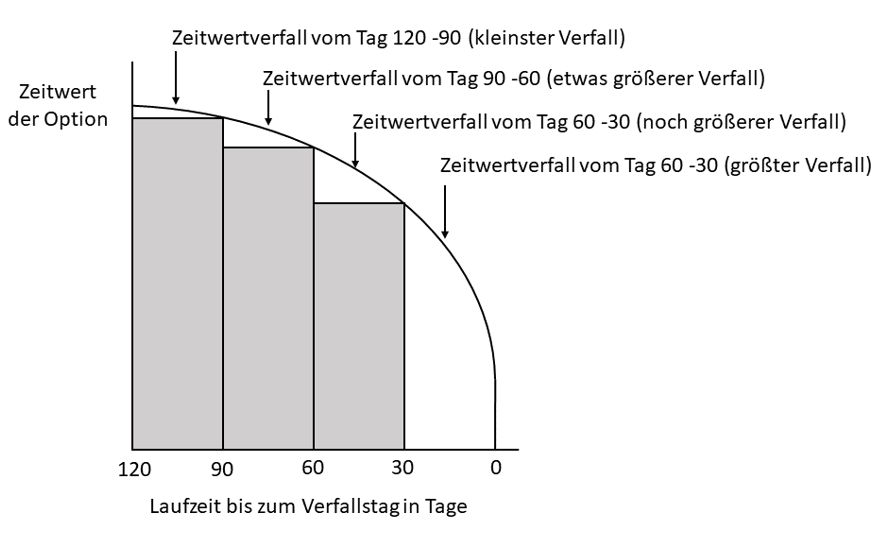
Der Zeitwertverfall nimmt zum Ende der Laufzeit hin immer weiter zu. Das bedeutet, wenn wir eine Option mit 100 Tagen Restlaufzeit haben, wird sich der Zeitwert am Anfang nur sehr langsam reduzieren. Je näher allerdings der Verfallstag rückt, desto größer wird das Theta und umso schneller wird der Zeitwert sinken.

In der Grafik ist dieses Verhalten noch einmal schematisch dargestellt. Der Zeitwertverfall ist in den ersten 30 Tagen (zwischen120 und 90 Tagen) am geringsten. Mit dem Fortschreiten der Zeit, reduziert sich der Zeitwert dann immer schneller. Die weißen Flächen kennzeichnen dabei den Zeitwertverfall. Aus der Grafik können wir ebenso erkennen, dass der Zeitwertverfall zwischen 30 und 0 Tagen am größten ist. Diese Eigenheit können wir uns als Optionsverkäufer zu Nutzen machen, indem wir überwiegend Optionen mit Laufzeiten in diesem Bereich verkaufen.

Als Optionsverkäufer profitieren wir von einem hohen Theta. Denn unser Ziel ist es, dass der Wert der Option so schnell wie möglich abnimmt und die Option am Ende der Laufzeit dann wertlos verfällt. Wir verkaufen also Optionen mit einer möglichst geringen Restlaufzeit (30 – 0 Tage). Als Optionskäufer hingegen, muss sich der Kurs innerhalb der Laufzeit unserer Prognose nach unserer Vorhersage entwickeln. Das bedeutet auch, dass die Zeit und schließlich auch das Theta immer gegen uns arbeitet. Denn mit jedem Tag der verstreicht, hat unsere Option weniger Zeit das Kursziel zu erreichen, bei dem unsere Option in die Gewinnzone rückt. Wir kaufen deshalb Optionen mit einer längeren Laufzeit.

Das Rho

Auch der risikofreie Marktzins wirkt sich auf den Optionspreis aus. Wie stark sich eine Veränderung des Zinses auf den Preis auswirkt, wird durch die Kennzahl Rho angegeben. Das Rho gibt folglich an, um wieviel sich der Optionspreis verändert, wenn sich der risikofreie Zinssatz (Zins für US-Staatsanleihen) um 1% verändert.

Beispiel: Hat eine Option ein Rho von 0,25 bedeutet es, dass der Wert der Option sich um 0,25€verändert, wenn sich der risikolose Zins um 1% verändert.

Für Call Optionen gilt: steigt der Zinssatz für US-Staatsanleihen um 1%, so steigt der Wert der Call-Option um die Größe des Rhos. Fällt der Zins, so fällt entsprechend auch der Wert der Option. Für Put Optionen hingegen gilt: steigen die Zinsen, so fällt der Wert der Put-Option um die Größe des Rhos und andersrum. Das Rho für Put-Optionen wird mit einem negativen Vorzeichen angegeben, das Rho für Call-Optionen mit einem Positiven.

Der Zinssatz beeinflusst den Optionspreis deshalb, weil der Stillhalter (Optionsverkäufer) das Kapital für eine eventuelle Ausübung vorhalten muss. Das bedeutet, er kann im Falle von Put-Optionen das Kapital nicht anderweitig investieren. Somit entgehen ihm Gewinne von mindestens der Höhe des risikofreien Marktzinses, den er z.B. für US Staatsanleihen bekommen hätte. Um diese Gewinne auszugleichen, wird der risikofreie Marktzins bei der Bildung des Optionspreises berücksichtigt.

Das Rho wirkt sich von allen „Griechen“ am wenigsten auf den Optionspreis aus und ist deshalb die unbedeutendste Kennzahl.

Fazit zu den Griechen

Als Griechen bezeichnet man Kennzahlen, welche für die Bildung des Optionspreises verantwortlich sind. Die Griechen sind vermutlich einer der häufigsten Gründe warum sich so wenig Anleger mit dem Thema Optionen befassen. Zugegebenermaßen ist es anfangs nicht ganz so leicht die verschiedenen Einflussfaktoren zu durchleuchten. Du solltest dich allerdings gerade am Anfang auch mit diesem Thema befassen, um dann beurteilen zu können, wie sich der Optionspreis in verschiedenen Marktsituationen verändern wird.

Auch wenn du im weiteren Verlauf nicht auf alle Griechen achtest, solltest du zumindest die drei Wichtigsten auf dem Schirm haben.

Delta: Das Delta ist die wichtigste Kennzahl. Auf diese wirst du beim Optionshandel zwangsläufig immer wieder treffen.

• Als Optionskäufer suchen wir ein möglichst hohes Delta.
• Als Optionsverkäufer suchen wir ein möglichst niedriges Delta.

Theta: Das Theta gehört ebenfalls zu den wichtigsten Kennzahlen. Insbesondere als Optionsverkäufer wollen wir schließlich wissen wie viel Geld wir pro Tag verdienen. Mit dem Theta haben wir die Möglichkeit verschiedene Laufzeiten der gleichen Option miteinander zu vergleichen und können dann entsprechend die Laufzeit mit dem höchsten Zeitwertverfall wählen.

• Als Optionskäufer profitieren wir von einem möglichst kleinen Theta.
• Als Optionsverkäufer profitieren wir von einem möglichst hohem Theta.

Vega: Die dritte Kennzahl, die du beachten solltest, ist das Vega. Alleine für die Auswahl der Optionsstrategie hilft es uns, wenn wir wissen wie sich eine Veränderung der Volatilität auf den Wert unserer Option auswirkt.

• Als Optionskäufer suchen wir einen Basiswert mit möglichst geringe Volatilität/ Vega.
• Als Optionsverkäufer suchen wir nach Basiswerten mit einer möglichst hohen Volatilität/ Vega.

Um mit Optionen sinnvoll handeln zu können, solltest du zumindest ein Startkapital von 5.000€ für den Optionshandel bereithalten. Hast du aktuell noch nicht soviel Kapital übrig, hilft dir mit Sicherheit ein Budgetplan, um deine Ausgaben im Blick zu behalten und diese zu reduzieren.

Weiterführende Informationen findest du unter anderen auf ESTABLY. Hier habe ich z.B. auch mein Optionsdepot und Handel meine Optionen.

Im nächsten Beitrag erfährst du alles rund um die Stillhaltergeschäfte.

Hast du Fragen zu den Griechen? Schreib es gerne unten in die Kommentare.